README.md

1632. Rank Transform of a Matrix

Given an m x nmatrix, return a new matrixanswerwhereanswer[row][col]is the rank ofmatrix[row][col].

The rank is an integer that represents how large an element is compared to other elements. It is calculated using the following rules:

• The rank is an integer starting from 1.
• If two elements p and q are in the same row or column, then:
  • If p < q then rank(p) < rank(q)
  • If p == q then rank(p) == rank(q)
  • If p > q then rank(p) > rank(q)
• The rank should be as small as possible.

The test cases are generated so that answer is unique under the given rules.

Example 1:

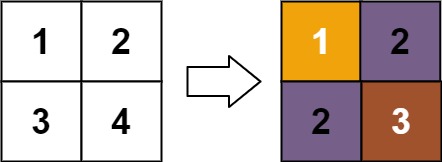
Input: matrix = [[1,2],[3,4]] Output: [[1,2],[2,3]] Explanation: The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column. The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1. The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1. The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2. 

Example 2:

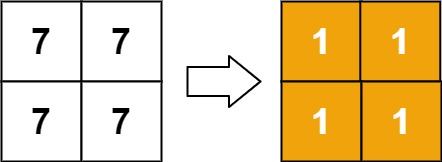
Input: matrix = [[7,7],[7,7]] Output: [[1,1],[1,1]] 

Example 3:

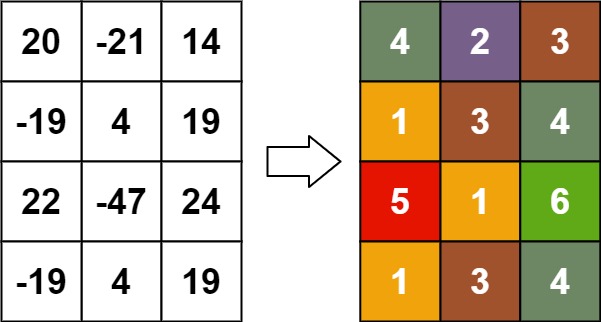
Input: matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]] Output: [[4,2,3],[1,3,4],[5,1,6],[1,3,4]] 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 500
• -109 <= matrix[row][col] <= 109

Solutions (Python)

1. Solution

classSolution: defmatrixRankTransform(self, matrix: List[List[int]]) ->List[List[int]]: m, n=len(matrix), len(matrix[0]) ranksr= [0] *mranksc= [0] *ncells=sorted((matrix[r][c], r, c) forrinrange(m) forcinrange(n)) parent= {} answermap= {} foriinrange(len(cells)): r, c=cells[i][1], cells[i][2] parent[(r, c)] = (r, c) answermap[(r, c)] =max(ranksr[r], ranksc[c]) +1ifi+1<len(cells) andcells[i][0] ==cells[i+1][0]: continuerowparent= {} colparent= {} for (r, c) inparent: ifrnotinrowparent: rowparent[r] = (r, c) whilerowparent[r] !=parent[rowparent[r]]: rowparent[r] =parent[rowparent[r]] ifanswermap[(r, c)] <=answermap[rowparent[r]]: parent[(r, c)] =rowparent[r] else: parent[rowparent[r]] = (r, c) ifcnotincolparent: colparent[c] = (r, c) whilecolparent[c] !=parent[colparent[c]]: colparent[c] =parent[colparent[c]] ifanswermap[parent[(r, c)]] <=answermap[colparent[c]]: parent[parent[(r, c)]] =colparent[c] else: parent[colparent[c]] =parent[(r, c)] for (r, c) inparent: whileparent[(r, c)] !=parent[parent[(r, c)]]: parent[(r, c)] =parent[parent[(r, c)]] answermap[(r, c)] =answermap[parent[(r, c)]] ranksr[r] =answermap[(r, c)] ranksc[c] =answermap[(r, c)] parent= {} return [[answermap[(r, c)] forcinrange(n)] forrinrange(m)]